| Temas |
|---|
| Aficiones |
| Biblioteca |
| Egipto y demás... |
| El Tiempo |
| Excursiones |
| Fotos |
| Física |
| Historia |
| Informática |
| Presentación |
8.-Cinemática
y dinámica relativista.
8.6.-Cantidad de movimiento relativista. La relatividad de la masa. En este apartado entramos realmente en materia (y nunca mejor dicho). Hasta ahora no nos hemos preocupado más que de aspectos cinemáticos y cuasi-filosóficos de la teoría de la relatividad restringida. Pero los cuerpos que se desplazan suelen tener masa, y empieza a ser momento (y nunca mejor dicho) de mirar qué sucede con ella... ¿Seguirá siendo la masa una propiedad característica propia de cada cuerpo, o sufrirá contracciones, dilataciones, o vaya usted a saber qué?... Un ejemplo nos sacará de dudas (!). Tomaremos como punto de partida un choque perfectamente elástico entre dos masas idénticas, que se acercan la una a la otra con velocidades iguales, pero de sentidos contrarios. En esas condiciones, el centro de masas de ambas partículas está quieto, y pondremos allí el origen de nuestro sistema de referencia fijo S. Como puede demostrarse fácilmente estudiando las ecuaciones del choque, las componentes x de las velocidades de ambas partículas no cambian, mientras que las componentes y simplemente cambian de signo. En la figura que se acompaña se ha prescindido del eje Z por comodidad de dibujo, ya que estudiamos el choque en dos dimensiones solamente. 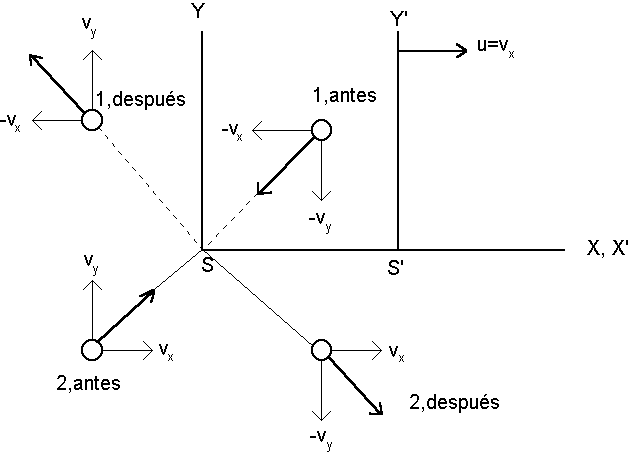
Δpy1 = mvy-(-mvy) = 2mvy Δpy2 = -mvy-mvy = -2mvy Y sumando, Δpy=0, tal como debe ser.
Respecto a las variaciones de p en el eje X', poco hay que decir. Los Δvx eran nulos en S, y lo seguirán siendo en S', según la ecuación primera de [22]:
y si los Δv'x son nulos, también lo son las variaciones de la cantidad de movimiento... Hasta aquí todo parece ir bien, pero al analizar las variaciones de py, las cosas se tuercen "un poco"... Usamos la ecuación segunda de [22], y ponemos vx negativo para la partícula 1 y positivo para la partícula 2, de acuerdo con sus valores. 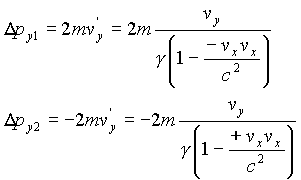 Las variaciones de la cantidad de movimiento para la componente y no son ni mucho menos iguales (véanse los denominadores), y al no anularse, obligan a reconsiderar nuestras ideas sobre la conservación de p. El dilema es decidir si aceptamos que el principio de conservación de la cantidad de movimiento es incompatible con la transformación de Lorentz, o bien si queremos cambiar la definición de p de forma que sí lo sea. De acuerdo con la coherencia de la teoría de la relatividad, no hay duda de que debemos optar por la segunda posibilidad, y redefinir p de forma que la ley de conservación sea invariante bajo una transformación de Lorentz. Si se consigue esta definición, la ley de conservación de p será válida en todos los sistemas inerciales, que es lo que deseamos para todas las leyes de la física. Para cambiar la definición de p, pensemos de dónde vienen nuestras dificultades con lo observado anteriormente.
Esta ecuación nos garantiza que la componente y de
vγ
será
la misma en todos los sistemas inerciales, que sólo se diferencian
entre sí en un factor constante de la velocidad según el
eje X. Por lo tanto, parece razonable utilizar este valor para redefinir
la cantidad de movimiento desde el punto de vista relativista como
La ecuación [25] permite una interpretación más compleja que la de la simple definición de p para que se adecue a la transformación de Lorentz.
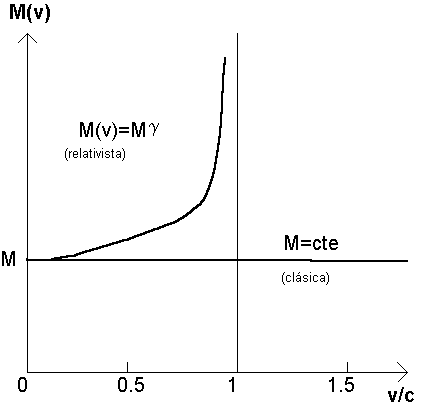
afirma que la masa de una partícula depende de la velocidad que
lleva. En reposo vale M, y aumenta a medida que aumenta su velocidad.
En el caso límite de v tendiendo a c,
la masa tiende a infinito, otra prueba más del valor límite
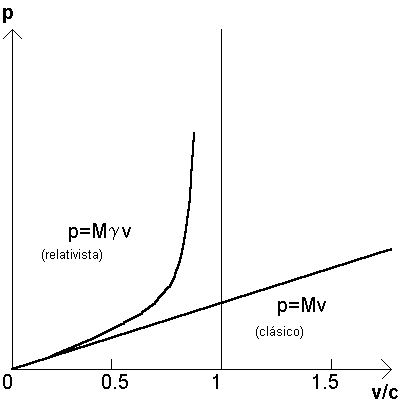
de c. ( Las figuras siguientes nos pueden ayudar a visualizar las diferencias
entre los conceptos clásicos y relativistas de la cantidad de movimiento
y de la masa.
El aumento de la masa en movimiento ha sido comprobado experimentalmente en repetidas ocasiones y fenómenos, constituye una pieza clave en el funcionamiento de los aceleradores rápidos de partículas, y es una de las predicciones de la teoría de la relatividad que más ha contribuido a la confirmación de su validez. |