Tema 04: Estática.	Subtema 02: Cuerpos en equilibrio.		04_02_003
Origen: No consta	Nivel: 2/3	Cuerpo colgado y apoyado
Una barra horizontal AB de 2 m de longitud y 40 Kg de masa se apoya en A en un pequeño resalte de una pared vertical. Está unida en B a un cable que tiene su otro extremo sujeto en la pared en un punto C a 1,5 m por encima de A. En el extremo B cuelga una masa de 20 Kg. Calculad la tensión del cable y las reacciones de la pared sobre la barra. Repetid el problema colgando la masa de 20 Kg justo en el centro de la barra.

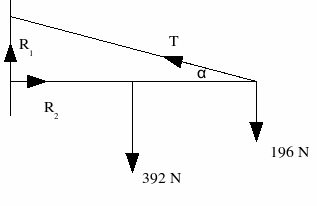
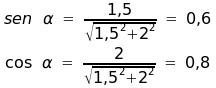S O L U C I Ó N:

(A)

Σ F_x = 0 ===> R₂ = T*0,8

Σ F_y = 0 ===> R₁ + T*0,6 = 392 + 196 = 588

Σ M_A = 0 ===> 392 * 1 + 196 * 2 = T * 0,6 * 2 (sólo la componente vertical de T produce momento respecto de A)

Resolviendo el sistema así formado se obtienen los valores siguientes:

T = 653 N ; R₁ = 196 N ; R₂ = 522 N

(B)

Si la masa de 20 Kg está en el centro, las ecuaciones del equilibrio se escriben así:

Σ F_x = 0 ===> R₂ = T*0,8

Σ F_y = 0 ===> R₁ + T*0,6 = 392 + 196 = 588

Σ M_A = 0 ===> 392 * 1 + 196 * 1 = T * 0,6 * 2

Y la solución del sistema resulta ahora:

T = 490 N ; R₁ = 294 N ; R₂ = 392 N

Como era de esperar, al acercarse la masa colgante hacia la pared, T y R₂ disminuyen, mientras que R₁ aumenta.

* * * * * * * * * *