Tema 05: Trabajo, energía y campo.	Subtema 02: Conservación de la energía.		05_02_002
Origen: Resnick I, 8,12	Nivel: UNI	Energía, rozamiento
Una partícula sin dimensiones, de masa m, comenzando en reposo va resbalando desde el punto más alto por la superficie de una esfera sólida sin rozamiento de radio R. Tomando como referencia el punto más alto para el ángulo y para la energía potencial, encontrad: (a)el cambio de energía potencial de la masa con respecto al ángulo (b)la energía cinética en función del ángulo (c)las aceleraciones tangencial y normal en función del ángulo, así como la aceleración total (d)el ángulo para el cual la masa se despega de la esfera (e)Si hay rozamiento (μ=0,5) entre la masa y la esfera, ¿ese ángulo de despegue es mayor o menor que antes? ¿Puede calcularse?

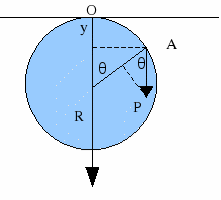
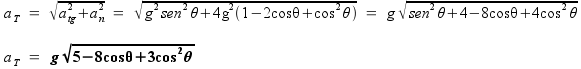S O L U C I Ó N:

(A)

E_PA = -mgy = -mg(R-Rcosθ) = -mgR(1-cosθ)

(B)

Como no hay rozamiento, 0 = E_PA + E_CA ===> E_CA = - E_PA = mgR(1-cosθ)

(C)

De la fórmula de la energía cinética E_C = ½ mv² se tiene que v = (2E_C / m)^1/2

(¡el mismo resultado que si se hiciese el problema sobre un plano inclinado sin rozamiento!)

(D)

La masa se separará de la esfera cuando la fuerza que provoca el giro (fuerza normal) se iguale con la componente normal de la reacción sobre la masa, es decir, cuando se cumpla que F_C = N = Pcosθ ===> mv²/R = mgcosθ ===>

(E)

Si hay rozamiento, la velocidad que va adquiriendo la masa que desciende es menor que antes, por lo que deberá descender más para poder despegarse.

Se cumplirá que 0 = E_PA + E_CA + F_r * OA ===>

0 = -mgR(1-cosθ) + ½ mv² + μmgcosθ(Rθ) ===>

v² = 2gR(1-cosθ) – 2μgcosθ Rθ

Deberá cumplirse, como antes, que mv²/R = mgcosθ ; con el nuevo valor de v² resultará la siguiente ecuación: 2 = 3cosθ+2μθcosθ, cuya resolución depende del valor concreto de μ. Dado que se nos dice que μ=0,5, quedará por resolver la ecuación 2 = 3cosθ+θcosθ

Puede resolverse de muchas maneras: por aproximaciones numéricas con una calculadora, dibujándola con una calculadora y buscando el primer cero, representándola en una hoja de cálculo, o con el Derive, o con el wxMaxima... en cualquier caso se obtiene como resultado aproximado el valor x = 1,055 rad = 60º.

* * * * * * * * * *