Tema 06: Campos: generalidades.	Subtema 01: Campo y potencial: el gradiente.		06_01_002
Origen: Edelvives, 6,8	Nivel: UNI	Campo potencial gradiente
Un campo vectorial conservativo viene dado por 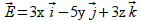a)Hallad su módulo y los ángulos que forma con los ejes de coordenadas en el punto (-1, 2, 0) b)En ese mismo punto, expresad el gradiente del potencial c)Hallad la diferencia de potencial entre los puntos (-1, 2, 0) y (0, 1, -1) d)Si el potencial es nulo en el origen de coordenadas, hallad su expresión general.

S O L U C I Ó N:

(A) E (-1, 2, 0) = (-3, -10, 0) ==>

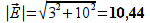
cos α = -3 / 10,44 ==> α = 107º

cos β = -10 / 10,44 ==> β = 163º

cos γ = 0 / 10,44 ==> γ = 90º

(B) Como 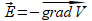se tendrá que

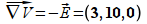
(C) Para calcular la función potencial V no hay más que integrar el campo, cambiado de signo; las componentes del campo son de variables separadas (por eso es conservativo...) y su integración es inmediata, obteniéndose

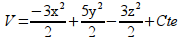A partir de esta expresión, se calcula el potencial en cada punto, teniendo que V_A (-1, 2, 0) = 17/2 + Cte , V_B (0, 1, -1) = 1 + Cte, de manera que su diferencia vale ΔV = 15/2

(D) Si V = 0 cuando x = y = z = 0, se obtiene que la Cte de integración es nula, así que

* * * * * * * * * *
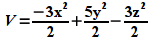